µ(t)=(cos(t)+cos(6t)/2+sin(14t)/3, sin(t)+sin(6t)/2+cos(14t)/3)
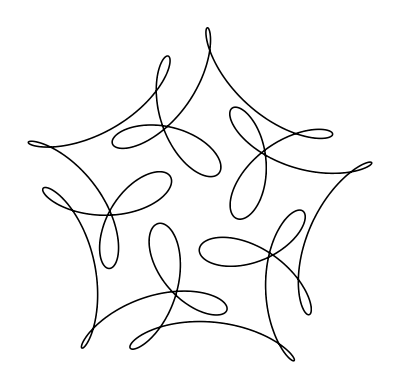 Where did the five-fold symmetry come from?
Where did the five-fold symmetry come from?
After I had studied wallpaper functions for several years, when I thought there could not possibly be anything to add to the story, at least from a mathematical point of view, an image appeared on my screen. I call it a moment of happy accident, since a random choice of wallpaper coefficients led to something that I think makes a pretty good story.
Impossible Wallpaper and Mystery Curves: Exploring Symmetry in Mathematics and Art
by Evelyn Lamb
Scientific American Blogs
http://blogs.scientificamerican.com/roots-of-unity/creating-symmetry-frank-farris/
I first heard of Frank Farris’s work a few years ago when he spoke at the Joint Mathematics Meetings about his art exhibition Seeing Symmetry, and I was immediately enchanted. A little while later, I read about his “impossible wallpaper,” which appears to have mathematically impossible five-fold rotational symmetry. Now he has published a book about his work, Creating Symmetry: the Artful Mathematics of Wallpaper Patterns. The book is a beautifully illustrated guide to fusing mathematical and artistic creativity to generate fascinating and visually appealing designs.
Creating Symmetry covers several different aspects of mathematics relating to symmetry. Broadly, Farris starts with symmetries of curves, moves to symmetries in the Euclidean plane, and ends by exploring analogous symmetries in spherical and hyperbolic geometry. Mathematically, the book incorporates complex analysis, Fourier series, abstract algebra, and modern geometry. Although that list looks daunting, there are no prerequisites. The explanations are self-contained and clear.
The first chapter introduces us to an enticing “mystery curve.” The mystery is not the formula for the curve but why it looks the way it does. The function is a combination of sines and cosines with a lot of sixes and fourteens floating around, but somehow it has five-fold rotational symmetry. “Take a moment to trace it with your eye and enjoy its dancing undulations,” Farris writes. “I hope that the figure—the ‘mystery curve’—surprises you.” This curve provides the impetus to delve deeper into exactly how the coefficients in combinations of trig functions affect the appearance of the resulting curves. (For more about curves like these, including an interactive curve generator, see Mike Croucher’s post, inspired by Farris and John D. Cook.)
As in the case of the mystery curve, visualizations drive the mathematics throughout the book. In one chapter, Farris writes,
“Happy accidents” like that one pop up several times in the book, and they help the reader understand how for Farris, mathematical and artistic creativity can fuel one another.
The majority of the book is devoted to wallpaper and frieze groups. Wallpaper groups describe patterns that have symmetry in two directions in the plane, and frieze groups describe patterns that have symmetry in one direction. These groups are appealing subjects, and there are many ways to learn about them, from algebra textbooks to Youtube videos.
To me, there are two main things that set Creating Symmetry apart. The first is how seamlessly geometry and algebra are united in describing these patterns. The second is color. It can be difficult to visualize transformations of the plane because the “graph” of such a transformation would live in four-dimensional space. A common way to get around this problem is to color the plane in some way and show pictures “before” and “after” the transformation. (See this video about Möbius transformations for a beautiful example of this approach.) Farris takes this idea and runs with it. Instead of using simple color wheels or square grids, Farris uses his own photographs, or, as he describes it, “the world as my color wheel.”
Farris’s approach to coloring the functions levels the playing field between math and art. Farris does not merely use color to illustrate mathematical functions, he uses mathematics to transform snapshots of landscapes, flowers, or dinner into beautiful designs. Math and design are equal partners. Farris uses some of the same color wheels multiple times, and it is fascinating to see how many different patterns can emerge from one source. My favorite color wheel was Kaiser Peach, pictured above, in part because of its story. Farris writes, “Climing Kaiser Peak Peak in the Sierra Nevada is a favorite pilgrimage, and taking a peach to the top is a traiditional way to make a peach taste especially wonderful.”
Farris’s color wheels inspire him to move beyond the 17 wallpaper and 7 frieze groups. By creating color wheels consisting of an image and its negative, rotated by 180 degrees, he introduces color-reversing symmetries. As the name suggests, in these symmetries, a transformation of the image ends up leaving shapes the same and colors switched to their negatives. By using “rotations” of colors instead of negatives, he generalizes this idea further to “color-turning” symmetries where, for example, a three-fold rotation of the plane takes orange to purple, purple to green, and green to orange.
Who is Creating Symmetry for? The book is not typical pop math fare. It has lots of equations and technical details in it, and I can see it functioning as a textbook in several different contexts: a supplement to complex analysis or abstract algebra or an organizing framework for an unusual undergraduate math elective that can delve into each topic more deeply. But although the book could be a textbook, it is still warm and friendly, and people without advanced math backgrounds can enjoy it as well, as long as they don’t mind skipping some well-signposted technical sections. Farris’s kindness, enthusiasm, and slightly quirky sense of humor (he reveals, for example, that he will pause a movie to examine the symmetry group of the wallpaper in the background) make what could have been a dry subject inviting. By the end, you may be ready to create symmetry for yourself.
The Artful Mathematics of Wallpaper Patterns
by Frank A. Farris
Princeton University Press
http://press.princeton.edu/titles/10435.html
This lavishly illustrated book provides a hands-on, step-by-step introduction to the intriguing mathematics of symmetry. Instead of breaking up patterns into blocks—a sort of potato-stamp method—Frank Farris offers a completely new waveform approach that enables you to create an endless variety of rosettes, friezes, and wallpaper patterns: dazzling art images where the beauty of nature meets the precision of mathematics.
Featuring more than 100 stunning color illustrations and requiring only a modest background in math, Creating Symmetry begins by addressing the enigma of a simple curve, whose curious symmetry seems unexplained by its formula. Farris describes how complex numbers unlock the mystery, and how they lead to the next steps on an engaging path to constructing waveforms. He explains how to devise waveforms for each of the 17 possible wallpaper types, and then guides you through a host of other fascinating topics in symmetry, such as color-reversing patterns, three-color patterns, polyhedral symmetry, and hyperbolic symmetry. Along the way, Farris demonstrates how to marry waveforms with photographic images to construct beautiful symmetry patterns as he gradually familiarizes you with more advanced mathematics, including group theory, functional analysis, and partial differential equations. As you progress through the book, you’ll learn how to create breathtaking art images of your own.
Fun, accessible, and challenging, Creating Symmetry features numerous examples and exercises throughout, as well as engaging discussions of the history behind the mathematics presented in the book.